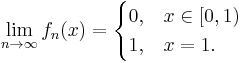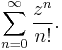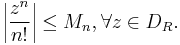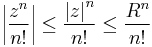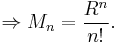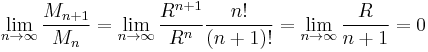Uniform convergence

In the mathematical field of analysis, uniform convergence is a type of convergence stronger than pointwise convergence. A sequence {fn} of functions converges uniformly to a limiting function f if the speed of convergence of fn(x) to f(x) does not depend on x.

The concept is important because several properties of the functions fn, such as continuity and Riemann integrability, are transferred to the limit f if the convergence is uniform.

Contents

History

Some historians claim that Augustin Louis Cauchy in 1821 published a false statement, but with a purported proof, that the pointwise limit of a sequence of continuous functions is always continuous; however, Lakatos offers a re-assessment of Cauchy's approach. Niels Henrik Abel in 1826 found purported counterexamples to this statement in the context of Fourier series, arguing that Cauchy's proof had to be incorrect. Cauchy ultimately responded in 1853 with a clarification of his 1821 formulation.

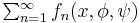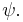The term uniform convergence was probably first used by Christoph Gudermann, in an 1838 paper on elliptic functions, where he employed the phrase "convergence in a uniform way" when the "mode of convergence" of a series \textstyle{\sum_{n=1}^\infty f_n(x,\phi,\psi)} is independent of the variables \phi and \psi. While he thought it a "remarkable fact" when a series converged in this way, he did not give a formal definition, nor use the property in any of his proofs.[1]

Later Gudermann's pupil Karl Weierstrass, who attended his course on elliptic functions in 1839–1840, coined the term gleichmäßig konvergent (German: uniformly convergent) which he used in his 1841 paper Zur Theorie der Potenzreihen, published in 1894. Independently a similar concept was used by Philipp Ludwig von Seidel[2] and George Gabriel Stokes but without having any major impact on further development. G. H. Hardy compares the three definitions in his paper Sir George Stokes and the concept of uniform convergence and remarks: Weierstrass's discovery was the earliest, and he alone fully realized its far-reaching importance as one of the fundamental ideas of analysis.

Under the influence of Weierstrass and Bernhard Riemann this concept and related questions were intensely studied at the end of the 19th century by Hermann Hankel, Paul du Bois-Reymond, Ulisse Dini, Cesare Arzelà and others.

Definition

Suppose S is a set and fn : S → R is a real-valued function for every natural number n. We say that the sequence (fn)n∈N is uniformly convergent with limit f : S → R if for every ε > 0, there exists a natural number N such that for all x ∈ S and all n ≥ N we have |fn(x) − f(x)| < ε.

Consider the sequence αn = supx |fn(x) − f(x)| where the supremum is taken over all x ∈ S. Clearly fn converges to f uniformly if and only if αn tends to 0.

The sequence (fn)n∈N is said to be locally uniformly convergent with limit f if for every x in some metric space S, there exists an r > 0 such that (fn) converges uniformly on B(x,r) ∩ S.

Notes

Note that interchanging the order of "there exists N" and "for all x" in the definition above results in a statement equivalent to the pointwise convergence of the sequence. That notion can be defined as follows: the sequence (fn) converges pointwise with limit f : S → R if and only if

for every x ∈ S and every ε > 0, there exists a natural number N such that for all n ≥ N one has |fn(x) − f(x)| < ε.

Here the order of the universal quantifiers for x and for ε is not important, but the order of the former and the existential quantifier for N is.

In the case of uniform convergence, N can only depend on ε, while in the case of pointwise convergence N may depend on both ε and x. It is therefore plain that uniform convergence implies pointwise convergence. The converse is not true, as the following example shows: take S to be the unit interval [0,1] and define fn(x) = xn for every natural number n. Then (fn) converges pointwise to the function f defined by f(x) = 0 if x < 1 and f(1) = 1. This convergence is not uniform: for instance for ε = 1/4, there exists no N as required by the definition. This is because solving for n gives n > log ε / log x. This depends on x as well as on ε. Also note that it is impossible to find a suitable bound for n that does not depend on x because for any nonzero value of ε, log ε / log x grows without bounds as x tends to 1.

Generalizations

One may straightforwardly extend the concept to functions S → M, where (M, d) is a metric space, by replacing |fn(x) − f(x)| with d(fn(x), f(x)).

The most general setting is the uniform convergence of nets of functions S → X, where X is a uniform space. We say that the net (fα) converges uniformly with limit f : S → X if and only if

for every entourage V in X, there exists an α0, such that for every x in I and every α ≥ α0: (fα(x), f(x)) is in V.

The above mentioned theorem, stating that the uniform limit of continuous functions is continuous, remains correct in these settings.

Definition in a hyperreal setting

Uniform convergence admits a simplified definition in a hyperreal setting. Thus, a sequence 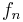f_n converges to f uniformly if for all x in the domain of f* and all infinite n, 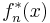f_n^*(x) is infinitely close to 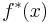f^*(x) (see microcontinuity for a similar definition of uniform continuity).

Examples

Given a topological space X, we can equip the space of bounded real or complex-valued functions over X with the uniform norm topology. Then uniform convergence simply means convergence in the uniform norm topology.

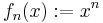The sequence f_n:[0,1]\rightarrow [0,1] with f_n(x):=x^n converges pointwise but not uniformly:

\lim_{n\rightarrow \infty}f_n(x) = \begin{cases} 0, & x \in [0,1) \\ 1, & x=1. \end{cases}

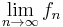In this example one can easily see that pointwise convergence does not preserve differentiability or continuity. While each function of the sequence is smooth, that is to say that for all n, f_n\in C^{\infty}([0,1]), the limit \lim_{n\rightarrow \infty}f_n is not even continuous.

Exponential function

The series expansion of the exponential function can be shown to be uniformly convergent on any bounded subset S of \mathbb{C} using the Weierstrass M-test.

Here is the series:

\sum_{n=0}^{\infty}\frac{z^n}{n!}.

Any bounded subset is a subset of some disc 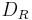D_R of radius R, centered on the origin in the complex plane. The Weierstrass M-test requires us to find an upper bound 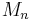M_n on the terms of the series, with 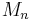M_n independent of the position in the disc:

\left| \frac{z^n}{n!}\right|\le M_n , \forall z\in D_R.

This is trivial:

\left| \frac{z^n}{n!}\right| \le \frac{\left| z\right|^n}{n!} \le \frac{R^n}{n!}
\Rightarrow M_n=\frac{R^n}{n!}.

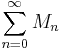If \sum_{n=0}^{\infty}M_n is convergent, then the M-test asserts that the original series is uniformly convergent.

The ratio test can be used here:

\lim_{n \to \infty}\frac{M_{n%2B1}}{M_n}=\lim_{n \to \infty}\frac{R^{n%2B1}}{R^n}\frac{n!}{(n%2B1)!}=\lim_{n \to \infty}\frac{R}{n%2B1}=0

which means the series over 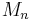M_n is convergent. Thus the original series converges uniformly for all 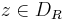z\in D_R, and since 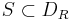S\subset D_R, the series is also uniformly convergent on S.

Properties

Applications

To continuity

See also: Uniform limit theorem

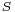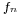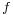If \scriptstyle S is a real interval (or indeed any topological space), we can talk about the continuity of the functions \scriptstyle f_n and \scriptstyle f. The following is the more important result about uniform convergence:

Uniform convergence theorem. If 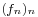\scriptstyle (f_n)_n is a sequence of continuous functions which converges uniformly towards the function 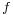\scriptstyle f on an interval 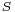\scriptstyle S, then 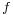\scriptstyle f is continuous on 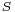\scriptstyle S as well.

This theorem is proved by the "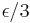\epsilon/3 trick", and is the archetypal example of this trick: to prove a given inequality (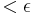<\epsilon), one uses the definitions of continuity and uniform convergence to produce 3 inequalities (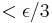<\epsilon/3), and then combines them via the triangle inequality to produce the desired inequality.

This theorem is important, since pointwise convergence of continuous functions is not enough to guarantee continuity of the limit function as the image illustrates.

More precisely, this theorem states that the uniform limit of uniformly continuous functions is uniformly continuous; for a locally compact space, continuity is equivalent to local uniform continuity, and thus the uniform limit of continuous functions is continuous.

To differentiability

If 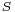\scriptstyle S is an interval and all the functions 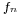\scriptstyle f_n are differentiable and converge to a limit 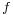\scriptstyle f, it is often desirable to differentiate the limit function 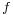\scriptstyle f by taking the limit of the derivatives of 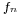\scriptstyle f_n. This is however in general not possible: even if the convergence is uniform, the limit function need not be differentiable, and even if it is differentiable, the derivative of the limit function need not be equal to the limit of the derivatives. Consider for instance 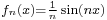\scriptstyle f_n(x) = \frac1n \sin(nx) with uniform limit 0, but the derivatives do not approach 0. The precise statement covering this situation is as follows:

If 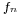\scriptstyle f_n converges uniformly to 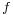\scriptstyle f, and if all the 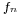\scriptstyle f_n are differentiable, and if the derivatives 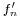\scriptstyle f '_n converge uniformly to g, then 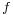\scriptstyle f is differentiable and its derivative is g.

To integrability

Similarly, one often wants to exchange integrals and limit processes. For the Riemann integral, this can be done if uniform convergence is assumed:

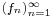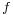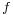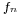If \scriptstyle (f_n)_{n=1}^\infty is a sequence of Riemann integrable functions which uniformly converge with limit \scriptstyle f, then \scriptstyle f is Riemann integrable and its integral can be computed as the limit of the integrals of the \scriptstyle f_n.

Much stronger theorems in this respect, which require not much more than pointwise convergence, can be obtained if one abandons the Riemann integral and uses the Lebesgue integral instead.

If 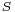\scriptstyle S is a compact interval (or in general a compact topological space), and 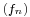\scriptstyle (f_n) is a monotone increasing sequence (meaning 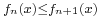\scriptstyle f_n(x) \leq f_{n%2B1}(x) for all n and x) of continuous functions with a pointwise limit \scriptstyle f which is also continuous, then the convergence is necessarily uniform (Dini's theorem). 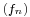Uniform convergence is also guaranteed if \scriptstyle S is a compact interval and \scriptstyle(f_n) is an equicontinuous sequence that converges pointwise.

Almost uniform convergence

If the domain of the functions is a measure space then the related notion of almost uniform convergence can be defined. We say a sequence of functions converges almost uniformly on E if there is a measurable subset F of E with arbitrarily small measure such that the sequence converges uniformly on the complement E \ F.

Note that almost uniform convergence of a sequence does not mean that the sequence converges uniformly almost everywhere as might be inferred from the name.

Egorov's theorem guarantees that on a finite measure space, a sequence of functions that converges almost everywhere also converges almost uniformly on the same set.

Almost uniform convergence implies almost everywhere convergence and convergence in measure.

See also

Notes

  1. ^ Jahnke, Hans Niels (2003). "6.7 The Foundation of Analysis in the 19th Century: Weierstrass". A history of analysis. AMS Bookstore. ISBN 978 0 82182623 2, p. 184. 
  2. ^ Lakatos, Imre (1976). Proofs and Refutations. Cambridge University Press. pp. 141. ISBN 052121078X. 

References

External links